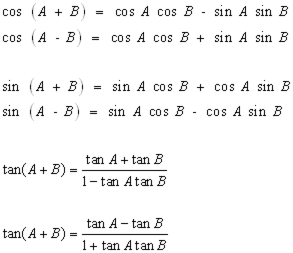I've been at it for a couple of days now... (I've been consulting Wikipedia's pages, haha...)
Original equation...
(r1 + r2)^2 = ((x2 - x1) - (bcr1 * cos(s1/bcr1 * t + θi1) - bcr2 * cos(s2/bcr2 * t + θi2)))^2 + ((y2 - y1) - (bcr1 * sin(s1/bcr1 * t + θi1) - bcr2 * sin(s2/bcr2 * t + θi2)))^2
...with the variables...
r1 = 2
x1 = 5
y1 = 7
bcr1 = 4
θi1 = 225
s1 = 3
r2 = 3
x2 = 8
y2 = 12
bcr2 = 3
θi2 = 45
s2 = 45
Latest progress...
24cos(1/12t + 180) + 24cos(3/4t + 225) + 40sin(3/4t + 225) = 18cos(2/3t + 45) + 30sin(2/3t + 45) + 34
I've used the Pythagorean identity a few times now, used the Angle Sum Identity, but can't think of how else I can simplify this.
(Obviously trying to solve for "t".)